Trasformer From Scratch
Published:
Introduction
Deep Learning has seen rapid progress recently with the introduction of Transformers, largely due to their ability to process data in parallel, unlike earlier models like RNNs, which processed data sequentially. Transformers have become the foundation for state-of-the-art generative models such as GPT-3, BERT, and T5. As a result, understanding how the Transformer model works is essential for anyone looking to contribute to the fields of artificial intelligence or deep learning. This blog begins by asking the question: “What is a Transformer?”.
What is a Transformer?
A Transformer is a neural architecture that computes data in parallel, utilizing an Attention mechanism. While parallel processing offers significant advantages, it can hinder the model’s ability to capture the sequential nature, or “context,” of data in tasks like natural language processing. To address this, Transformers use positional encoding, which incorporates sequential information by adding position vectors to the input data.
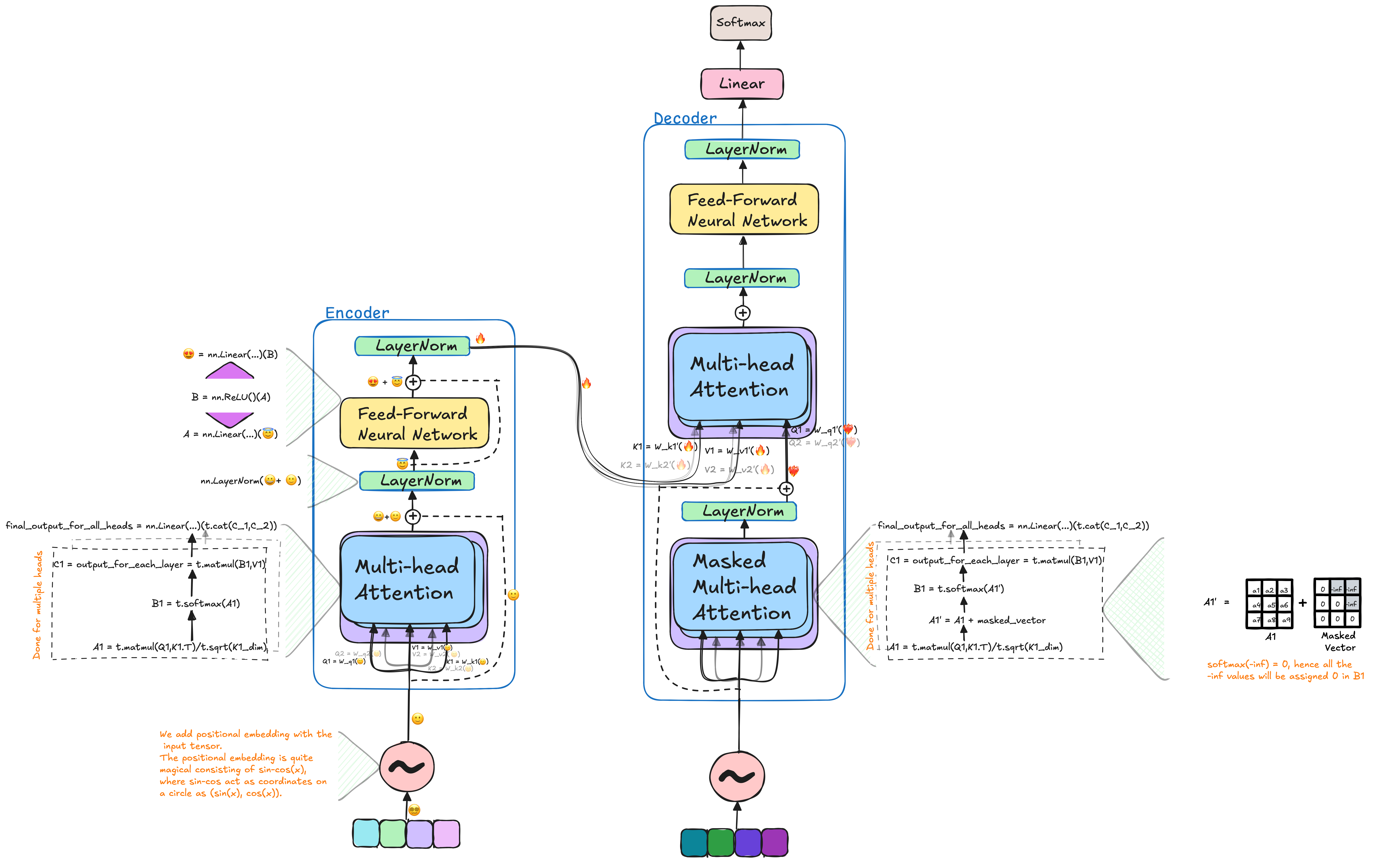
The Transformer model consists of two primary components: the encoder and the decoder. The encoder processes input data and passes it to the decoder. The decoder then uses both the encoder’s processed input and previous predictions to predict the next elements in a sequence. To fully understand the architecture of the Transformer, we will first explore its individual components, starting with Positional Encoding.
🧿 Positional Encoding
Positional encoding is essential for the Transformer model because it enables the model to recognize the sequential nature of input data. Since the data is processed in parallel, the sequence information would otherwise be lost. To address this, each word in a sentence needs a representation that captures its position.
In traditional binary systems, the least significant bit (LSB) alternates with every number, the second-lowest bit alternates every two numbers, and so on. However, using binary representations is inefficient in a world dominated by floating-point numbers. Instead, we can use continuous float equivalents—sinusoidal functions—that serve a similar purpose, acting like alternating bits.
By adding positional embeddings, the model gains a sense of sequence using the following formula:
\[PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\] \[PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)\]Here, $pos$ represents the position of the word in the sentence, $i$ is the dimension index, and $d_{model}$ is the dimensionality of the embedding. This can be implemented easily using the following code:
def position_embedding(self, sent: Tensor, d_model: int) -> Tensor:
pe = np.zeros((sent.size()[0], d_model))
for pos, word in enumerate(sent.size()[0]):
for i in range(0,d_model, 2):
pe[pos][i] = math.sin(pos/(10000**(2*i/d_model)))
pe[pos][i+1] = math.cos(pos/(10000**(2*i/d_model)))
# adding positional encoding to the sentence, that will be passed into the transformer (encoder/decoder).
final_sent = sent + pe
return t.tensor(final_sent)
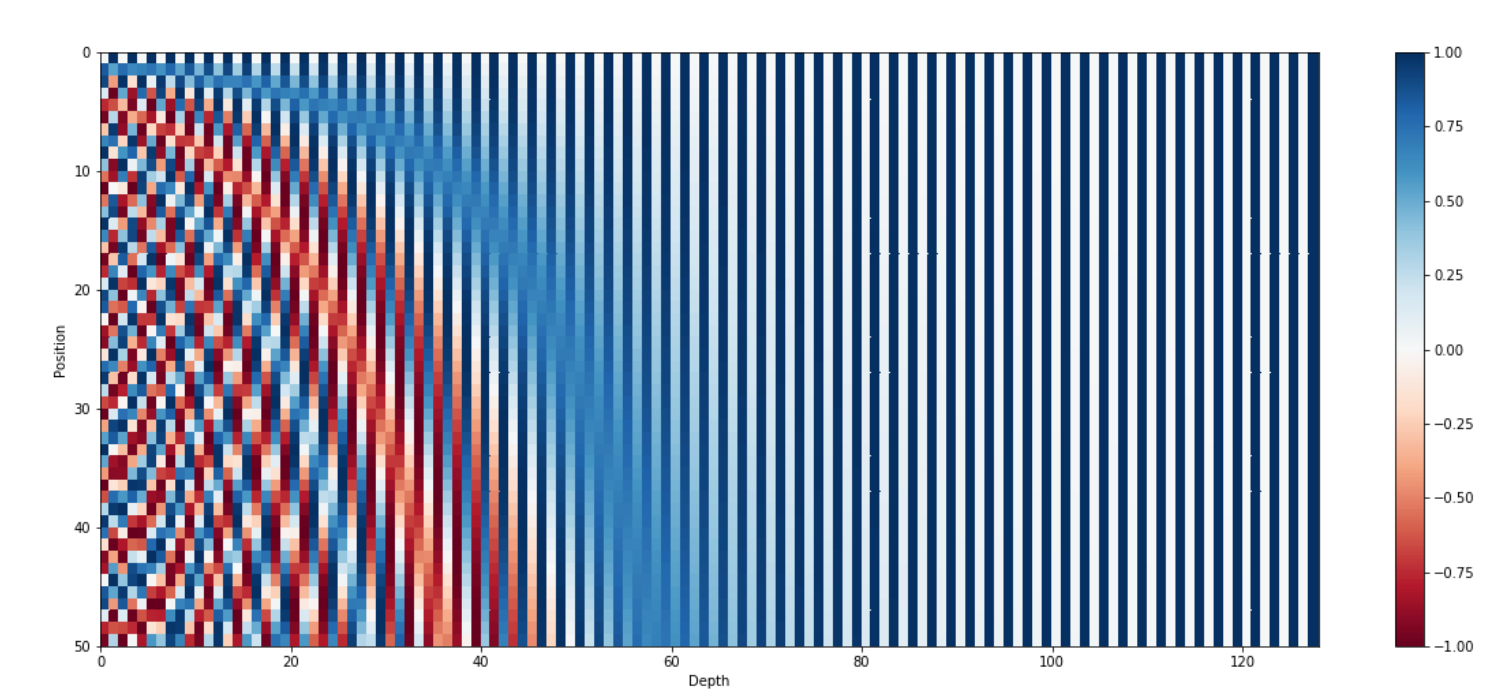
Figure 1 - The 128-dimensional positonal encoding for a sentence with the maximum lenght of 50. Each row represents the embedding vector [1].
These positional encodings are added in case of both the modules of the transformer, i.e., the encoder and the decoder.
🍀🎃 Encoder
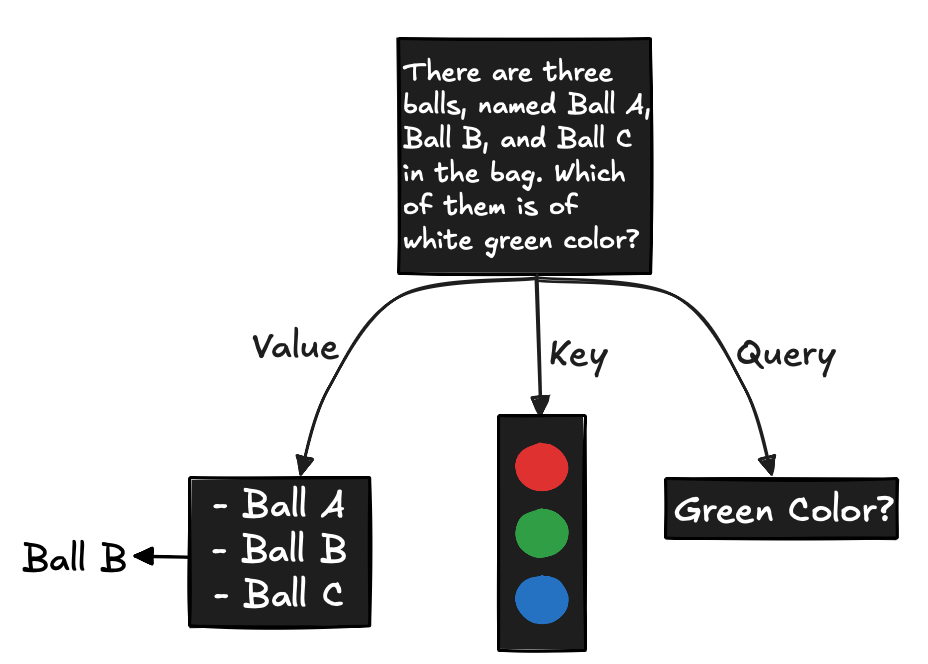
Key, Value, and Query in Transformers
Another important concept in Transformers is the role of “key,” “value,” and “query.” These components drive the self-attention mechanism, which is a core feature of the model.
- Query: The query can be thought of as the question being asked by the model.
- Key: The keys serve as the context or references that the model uses to determine how closely a query matches.
- Value: The values contain the actual information or answers, and the most relevant value is selected based on the similarity between the query and the keys.
This process allows the model to focus on the most important parts of the input sequence by aligning queries with matching keys and then retrieving the corresponding values.
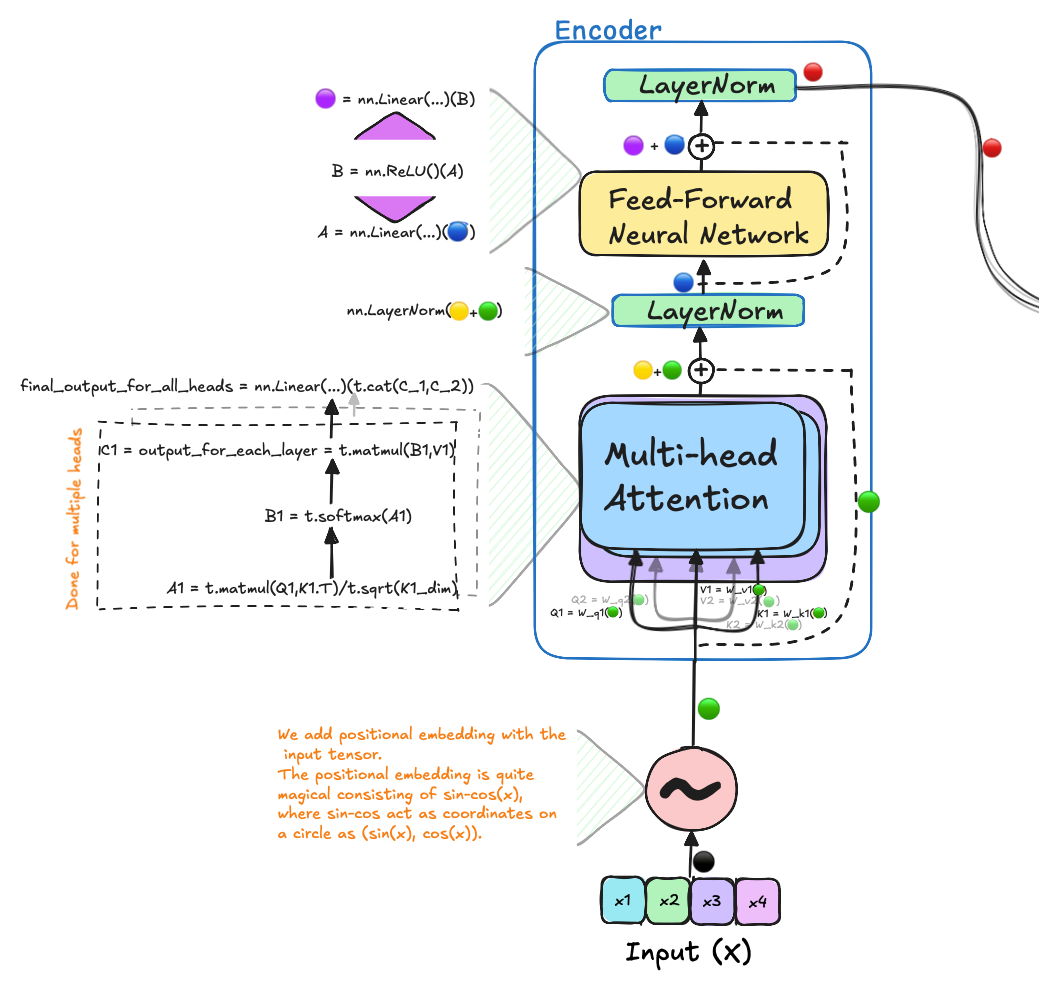
Key Components of the Transformer Encoder
The Transformer encoder is composed of several components that work together to process and encode the input data. These include:
- Multi-Head Attention: This mechanism allows the model to focus on different parts of the input simultaneously, capturing diverse relationships between words in a sentence.
- Layer Normalization (LayerNorm): This helps stabilize and normalize the activations in each layer, improving training and convergence.
- Feed-Forward Layers: These layers perform additional transformations on the data to enhance its representation, helping the model capture complex patterns.
In the next sections, we will dive deeper into each of these components to understand how they contribute to the overall performance of the Transformer model.
🐷 Multi-Head Attention
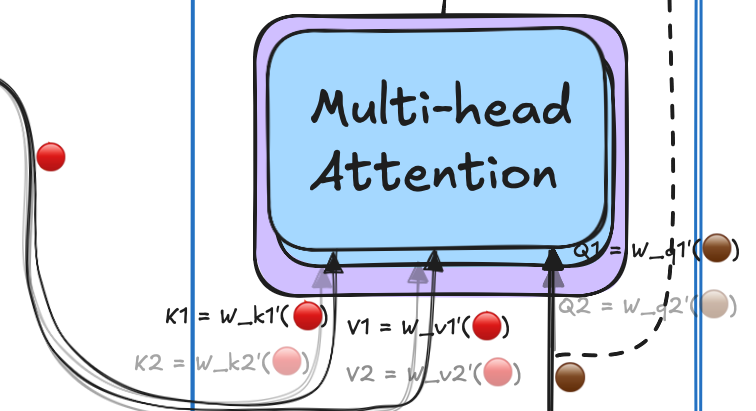
In the multi-head attention mechanism, several matrices like W_q, W_k, and W_v are used to extract information from input embeddings, transforming them into queries, keys, and values. The key advantage of having multiple heads is that it allows the model to capture different aspects of the context for each query. Imagine a student being able to ask multiple questions (multiple heads) versus just one question (single head), enabling a deeper and more nuanced understanding of the input data.
The outputs from all heads are concatenated and passed through a linear layer that projects them back into the original dimension.
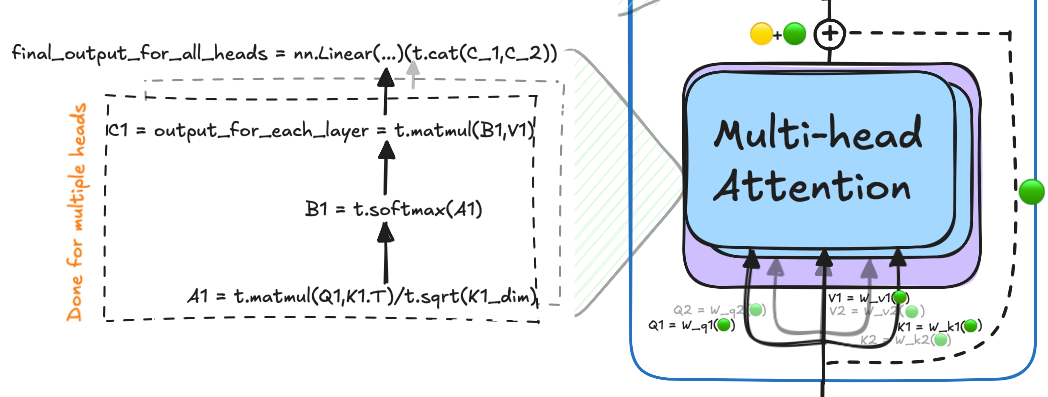
Here’s an example of how multi-head attention works in code:
def self_attention(self):
query = self.W_q(self.input_embedding).view(1, self.num_heads, self.seq_len, self.q_dim) # (1, 2, 4, 512)
key = self.W_k(self.input_embedding).view(1, self.num_heads, self.seq_len, self.k_dim) # (1, 2, 4, 512)
value = self.W_v(self.input_embedding).view(1, self.num_heads, self.seq_len, self.v_dim) # (1, 2, 4, 512)
# Compute similarity score
attention_score = t.softmax(t.matmul(query, key.transpose(2, 3)) / t.sqrt(t.tensor(self.k_dim)), dim=-1) # (1, 2, 4, 4)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim * self.num_heads) # (1, 4, 512)
final_attention = self.W_o(overall_attention) # (1, 4, 512)
return final_attention
🤥 LayerNorm
Layer normalization is a critical component in transformers, designed to stabilize and accelerate the training process. It normalizes the inputs to each layer, ensuring a mean of zero and a standard deviation of one. This technique helps to maintain a stable distribution of activations during training, leading to more consistent learning. The benefits of layer normalization include:
- Reducing Internal Covariate Shift: By normalizing inputs, it ensures the distribution remains constant, improving convergence.
- Improving Gradient Flow: Helps address issues with vanishing or exploding gradients, critical for deep networks like transformers.
- Faster Convergence: Leads to quicker training, often requiring fewer epochs.
- Independence from Batch Size: Unlike batch normalization, layer normalization works at the feature level for individual samples, making it ideal for variable sequence lengths.
- Facilitating Larger Learning Rates: The stable dynamics allow for larger learning rates, accelerating training.
- Enhancing Generalization: Helps in reducing overfitting, acting as a form of regularization.
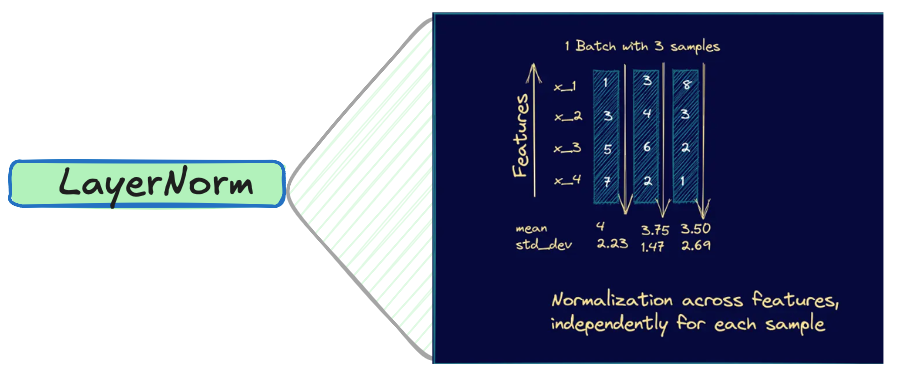
The code for LayerNorm is straightforward:
self.layer_norm = nn.LayerNorm(512)
🥳 Feed-Forward Layers
The feed-forward layers in a transformer consist of two linear layers with a ReLU activation in between. The first layer projects the input into a higher dimension, and the second layer brings it back to the original size. This simple yet powerful architecture allows the model to transform and refine the representation of data.
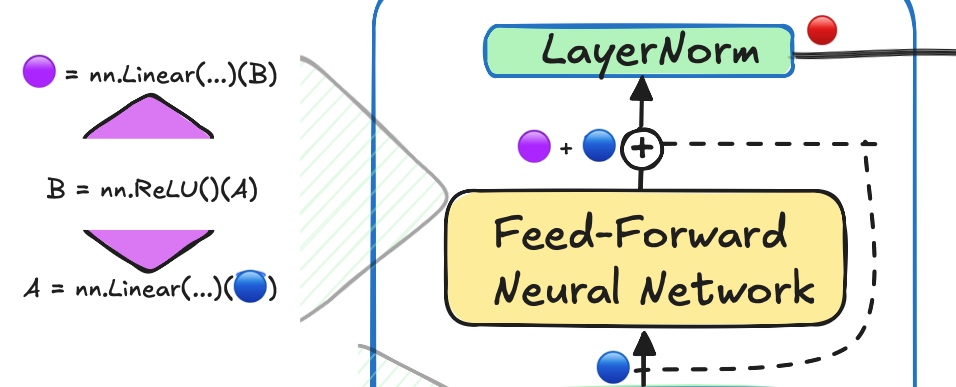
Here’s an implementation of the feed-forward module:
def ffn(self, x: Tensor) -> Tensor:
x1 = self.fc1(x)
x2 = self.relu(x1)
x3 = self.fc2(x2)
return x3
Full Encoder Implementation
Now that we’ve discussed the key components, here is the full implementation of an encoder in PyTorch:
class encoder:
def __init__(self, num_heads: int, sent: Tensor) -> None:
super(encoder, self).__init__()
self.sent = sent
self.num_heads = num_heads
self.k_dim = 512; self.v_dim = 512; self.q_dim = 512
self.W_q = nn.Linear(512, self.k_dim * self.num_heads)
self.W_k = nn.Linear(512, self.k_dim * self.num_heads)
self.W_v = nn.Linear(512, self.v_dim * self.num_heads)
self.seq_len = sent.size()[0]
assert self.seq_len == 4, "The sequence length should be 4."
self.W_o = nn.Linear(512 * self.num_heads, 512)
self.layer_norm = nn.LayerNorm(512)
self.fc1 = nn.Linear(512, 1024)
self.fc2 = nn.Linear(1024, 512)
self.relu = nn.ReLU()
def self_attention(self):
query = self.W_q(self.input_embedding).view(1, self.num_heads, self.seq_len, self.q_dim) # (1, 2, 4, 512)
key = self.W_k(self.input_embedding).view(1, self.num_heads, self.seq_len, self.k_dim) # (1, 2, 4, 512)
value = self.W_v(self.input_embedding).view(1, self.num_heads, self.seq_len, self.v_dim) # (1, 2, 4, 512)
# Compute similarity score
attention_score = t.softmax(t.matmul(query, key.transpose(2, 3)) / t.sqrt(t.tensor(self.k_dim)), dim=-1) # (1, 2, 4, 4)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim * self.num_heads) # (1, 4, 512)
final_attention = self.W_o(overall_attention) # (1, 4, 512)
return final_attention
def ffn(self, x: Tensor) -> Tensor:
x1 = self.fc1(x)
x2 = self.relu(x1)
x3 = self.fc2(x2)
return x3
def forward(self):
self.input_embedding = self.position_embedding(self.sent, 4)
multi_head_attn = self.self_attention()
multi_head_attn_out = self.W_o(multi_head_attn)
input_embedding = self.layer_norm(multi_head_attn_out + self.input_embedding)
ffn_out = self.ffn(input_embedding)
encoder_out = self.layer_norm(ffn_out + input_embedding)
return encoder_out
This is the complete encoder structure with multi-head attention, layer normalization, and feed-forward layers. These core components allow the Transformer to learn complex representations and perform powerful sequence-to-sequence modeling.
🐳🐙 Decoder
The decoder architecture is often one of the least explained aspects in related materials, with limited information available about how the decoder interacts with the encoder. Therefore, this section aims to provide a detailed explanation to clarify the decoder’s role and operation. Certain components that are identical to the encoder, such as the Feed-Forward Network and Multi-Head Attention, are not covered in depth here.
The decoder takes the output or ground-truth sentence as input and adds positional embeddings before passing it through the masked multi-head attention module.
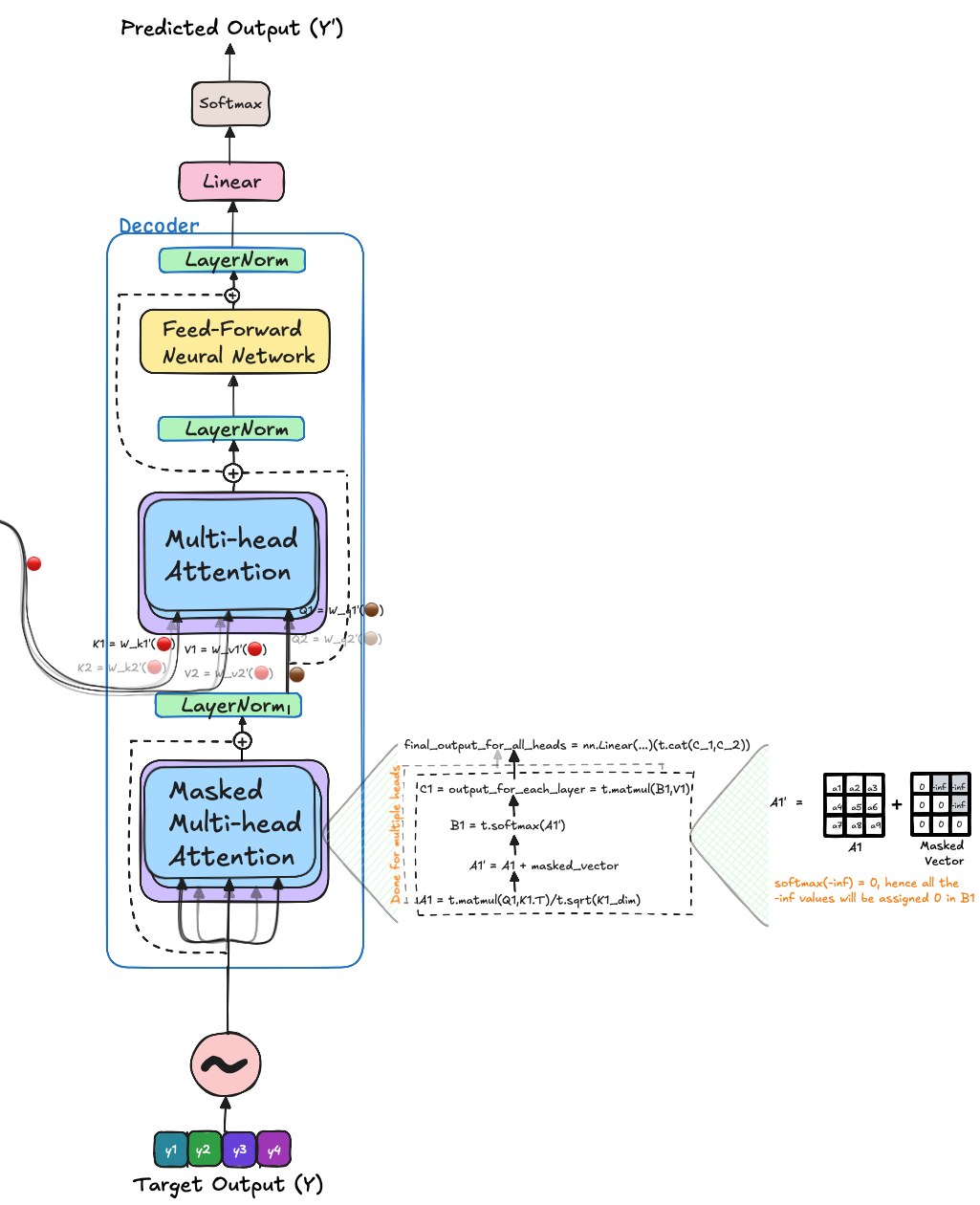
🐸 Masked Multi-Head Attention
In the masked multi-head attention module, the input is the sentence with added positional embeddings. The attention mechanism works similarly to the encoder, using “query,” “key,” and “value.” However, the key difference is the inclusion of a masking tensor. This mask ensures that the model cannot access future token representations when predicting the next token, relying only on past information.
The masking tensor is constructed with values of $0$ and $-\infty$ for the upper right part of the matrix. This is added to the product of the query and key, keeping the lower left values (including the diagonal) intact while setting the upper right values to infinity. After applying softmax, these $-\infty$ elements are converted to $0$, effectively hiding future tokens for each word. Finally, we incorporate the values, of the word with non-zero values by taking product between masked key-query product values t.matmul(B1,V1) as output of this module. Finally, similar to multi-head attention, the information for all the heads are concatenated and filtered through a linear layer.
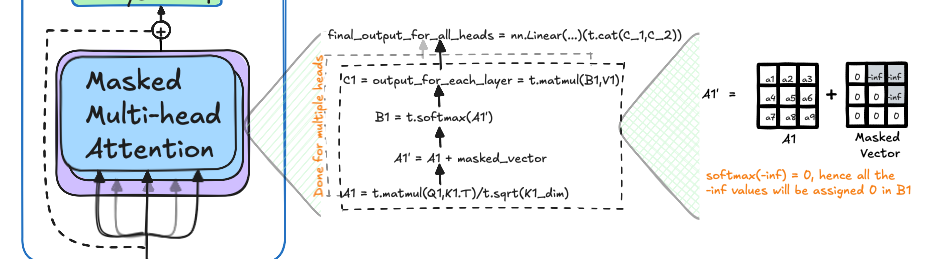
def masked_multi_head_attention(self, encoder_output: Tensor, dec_attn: Tensor) -> Tensor:
'''
We are making this as the masked multi-head attention, as we are masking the future words in the sentence.
For reference you can look at its diagram before implementation to get an intuition about it.
'''
query = self.W_q_m(dec_attn).view(1, self.num_heads, self.seq_len, self.q_dim)
key = self.W_k_v_m(encoder_output).view(1, self.num_heads, self.seq_len, self.k_dim)
value = self.W_k_v_m(encoder_output).view(1, self.num_heads, self.seq_len, self.v_dim)
attention_score = t.matmul(query, key.transpose(2,3))/t.sqrt(t.tensor(self.k_dim))
# Adding the attention score with the masking tensor to mask the future words in the sentence.
attention_score = t.softmax((attention_score + self.masking_tensor), dim = -1)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim*self.num_heads)
final_attention = self.W_o_m(overall_attention)
return final_attention
🦃 Multi-Head Attention
In this module, the multi-head attention functions similarly to how it does in the decoder. The key difference lies in the inputs it receives. The encoder_output is used to construct the keys and values, while the query is derived from the output of the masked multi-head attention module. This setup allows the model to incorporate information from the input sentence (through the keys and values) while utilizing the available context from the ground-truth to predict the next word.
def multi_head_attention(self, encoder_output: Tensor, dec_attn: Tensor) -> Tensor:
'''
We are making this function for just 1 sample.
The words of which will be computed to have similarity with each other.
The query, key, and value are the three vectors that are used to computed with the embedding layer dim to assign a new dim.
'''
query = self.W_q(dec_attn).view(1, self.num_heads, self.seq_len, self.q_dim)
key = self.W_k(encoder_output).view(1, self.num_heads, self.seq_len, self.k_dim)
value = self.W_v(encoder_output).view(1, self.num_heads, self.seq_len, self.v_dim)
attention_score = t.matmul(query, key.transpose(2,3))/t.sqrt(t.tensor(self.k_dim))
# Adding the attention score with the masking tensor to mask the future words in the sentence.
attention_score = t.softmax((attention_score + self.masking_tensor), dim = -1)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim*self.num_heads)
final_attention = self.W_o_m(overall_attention)
return final_attention
The whole code for decoder can be found below:
class decoder:
def __init__(self, num_heads: int, out_sent: Tensor, encoder_output: Tensor) -> None:
super(decoder, self).__init__()
self.out_sent = out_sent
self.num_heads = num_heads
'''
We are making output dim same as the input dim,
as we are taking 2 heads for multi-head attention,
as a result, 1024/2 = 512 for the output dim.
The will become 1024 when it will be concatenated.
'''
self.encoder_output = encoder_output
self.k_dim = 512; self.v_dim = 512; self.q_dim = 512
self.W_q = nn.Linear(512, self.k_dim*self.num_heads)
self.W_k = nn.Linear(512, self.k_dim*self.num_heads)
self.W_v = nn.Linear(512, self.v_dim*self.num_heads)
self.W_q_m = nn.Linear(512, self.k_dim*self.num_heads)
self.W_k_m = nn.Linear(512, self.k_dim*self.num_heads)
self.W_v_m = nn.Linear(512, self.v_dim*self.num_heads)
self.masking_tensor = t.triu(t.full((1, self.num_heads, self.seq_len, self.seq_len), float("inf")), diagonal = 1)
self.seq_len = out_sent.size()[0]
assert self.seq_len == 4, "The sequence length should be 4."
self.W_o = nn.Linear(512*self.num_heads,512)
self.W_o_m = nn.Linear(512*self.num_heads,512)
self.layer_norm = nn.LayerNorm(512)
self.fc1 = nn.Linear(512, 1024)
self.fc2 = nn.Linear(1024, 512)
self.relu = nn.ReLU()
def position_embedding(self, sent: Tensor, d_model: int) -> Tensor:
'''
Defined in depth in the encoder.py file.
'''
pe = np.zeros((sent.size()[0], d_model))
for pos, word in enumerate(sent.size()[0]):
for i in range(0,d_model, 2):
pe[pos][i] = math.sin(pos/(10000**(2*i/d_model)))
pe[pos][i+1] = math.cos(pos/(10000**(2*i/d_model)))
# adding positional encoding to the sentence, that will be passed into the transformer (encoder/decoder).
final_sent = sent + pe
return t.tensor(final_sent)
def ffn(self, x:Tensor) -> Tensor:
x1 = self.fc1(x)
x2 = self.relu(x1)
x3 = self.fc2(x2)
return x3
def masked_multi_head_attention(self) -> Tensor:
'''
We are making this as the masked multi-head attention, as we are masking the future words in the sentence.
For reference you can look at its diagram before implementation to get an intuition about it.
'''
query = self.W_q_m(self.input_embedding).view(1, self.num_heads, self.seq_len, self.q_dim) # (1, 2, 4, 512)
key = self.W_k_m(self.input_embedding).view(1, self.num_heads, self.seq_len, self.k_dim) # (1, 2, 4, 512)
value = self.W_v_m(self.input_embedding).view(1, self.num_heads, self.seq_len, self.v_dim) # (1, 2, 4, 512)
# we will take the dot product of query and key to get the similarity score.
attention_score = t.softmax(t.matmul(query, key.transpose(2,3))/t.sqrt(t.tensor(self.k_dim)), dim=-1) # (1, 2, 4, 4)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim*self.num_heads) # (1, 4, 512)
final_attention = self.W_o(overall_attention) # (1, 4, 512)
return final_attention
def multi_head_attention(self, encoder_output: Tensor, dec_attn: Tensor) -> Tensor:
'''
We are making this function for just 1 sample.
The words of which will be computed to have similarity with each other.
The query, key, and value are the three vectors that are used to computed with the embedding layer dim to assign a new dim.
'''
query = self.W_q(dec_attn).view(1, self.num_heads, self.seq_len, self.q_dim)
key = self.W_k(encoder_output).view(1, self.num_heads, self.seq_len, self.k_dim)
value = self.W_v(encoder_output).view(1, self.num_heads, self.seq_len, self.v_dim)
attention_score = t.matmul(query, key.transpose(2,3))/t.sqrt(t.tensor(self.k_dim))
# Adding the attention score with the masking tensor to mask the future words in the sentence.
attention_score = t.softmax((attention_score + self.masking_tensor), dim = -1)
overall_attention = t.matmul(attention_score, value)
overall_attention = t.cat(overall_attention).view(1, self.seq_len, self.k_dim*self.num_heads)
final_attention = self.W_o_m(overall_attention)
return final_attention
def forward(self) -> Tensor:
x = self.input_embedding = self.position_embedding(self.out_sent, 512)
x_ = self.masked_multi_head_attention()
x = self.layer_norm(x_ + x)
x_ = self.multi_head_attention(self.encoder_output, x)
x = self.layer_norm(x + x_)
x_ = self.ffn(x)
x = self.layer_norm(x_ + x)
return x
🍾👨🎓 Exercise to understand Architecture in Depth.
- TBW
🎀🙇🏻 Acknowledgements:
I am grateful to Dr. Michael Sklar and Atif Hassan for helping me during the prepartion of this repository. I am also grateful to family, friends and online resources mentioned:
- Transformer Architecture: The Positional Encoding by Amirhossein Kazemnejad’s
- What is Masked multi-head attention?
- Transformer Neural Network explained by CodeEmporium
- Transformer Playslist by CodeEmporium
- The Illustrated Transformer by Jay Alammar

